chebyshev.mws
syntfil[Chebyshev]
- výpočet Čebyševovy aproximace
Calling sequence:
Chebyshev(order, Os, ap, var)
Parameters:
order -
stupeň Čebyševovy aproximace [-]
Os -
kmitočet hranice nepropustného pásma [1/s]
ap -
maximální útlum v propustném pásmu [dB]
var -
symbol proměnné provozního činitele přenosu a charakteristické funkce
Parametr
order
musí být celé kladné číslo, parametr
ap
musí být kladná reálné číslo a parametr
var
musí být typu
symbol
. Parametr
Os
není ve funkci využíván a nekontroluje se jeho typ.
Description:
-
Funkce vrací posloupnost provozního činitele přenosu G a charakteristické funkce
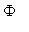 .
.
-
Provozní činitel přenosu G má tvar polynomu s proměnnou
var
stupně
order
.
-
Přenosová funkce
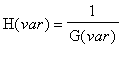
-
Charakteristická funkce má tvar
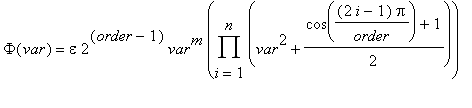 , kde
, kde
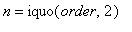 a
a
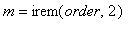
-
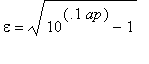
Info level:
Změnou proměnné
infolevel[syntfil]
dostanete podrobnější výsledek.
infolevel[syntfil] =
2 -
vypsání polynomů provozního činitele přenosu a charakteristické funkce na oddělených řádcích s textovým označením
3 -
jako úroveň 2 + vypsání pólů přenosové funkce a parametru
4 -
jako úroveň 3 + vypsání parametrů elipsy na které leží nuly provozního činitele přenosu a vypsání nul charakteristické funkce
Example:
![`You can set infolevel[syntfil] variable to 2..5 to get more detailed results!`](images/chebyshev9.gif)
![infolevel[syntfil] := 3](images/chebyshev10.gif)
epsilon = .9976283451
Poles of H:
[-.8517039862e-1+.9464844330*j, -.8517039862e-1-.9464844330*j, -.2056195314+.3920466889*j, -.2056195314-.3920466889*j]
Chebyshev:
G = 1.412537545+7.981026761*s^4+4.641604426*s^3+9.330758585*s^2+3.230463838*s
Phi = .9976283450+7.981026761*s^4+7.981026761*s^2
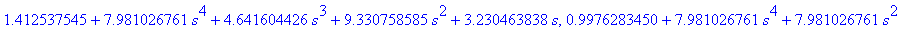
| > |
G,Phi:=Chebyshev(4,2,3,s);
|
![infolevel[syntfil] := 1](images/chebyshev12.gif)
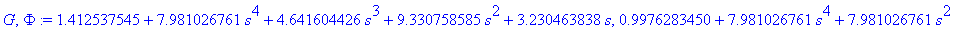
Zobrazení průběhu modulové frekvenční charakteristiky
| > |
plot(MagnitudeHdB(1/G)(omega),omega=0..3);
|
![[Maple Plot]](images/chebyshev14.gif)
See also:
ChebyshevNLPOrder
ChebyshevPoles,
Chebyshev_asnew
DroppNLP,
TestCharEqn,
MagnitudeH,
MagnitudeHdB,
PhaseH,
GroupDelayH
kromě Čebyševovy aproximace lze použít další aproximace
Butterworth,
InvChebyschev,
InvChebyshevB,
Cauer,
CauerB,
CauerC
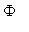 .
.
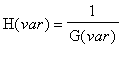
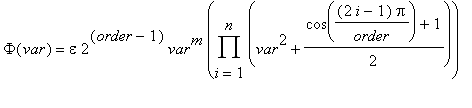 , kde
, kde
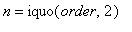 a
a
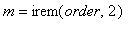
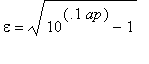
![]()
![[Maple Plot]](images/chebyshev14.gif)