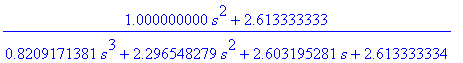droppnlp.html

droppnlp.mws

syntfil[DroppNLP] - výpočet prvků LC příčkového filtru typu normovaná dolní propust (NDP)

Calling sequence:

DroppNLP(termination, R, direction, struct, pol, chpol)

DroppNLP(termination, R, direction, struct, pol, chpol, zeros)

Parameters:

termination - zakončení NDP ( common - standardní, open - naprázdno, short - zkrat)

R - velikost normovaného zakončovacího rezistoru (R=1)

direction - směr zpracování NDP ( front - od prvního prvku, rear - od posledního prvku)

struct - struktura NDP (struktura začína ze předu PI - příčným kapacitorem, T - podélným induktorem)

pol - provozní činitel přenosu

chpol - charakteristická funkce

zeros - (volitelný parametr) jednorozměrné pole nulových bodů přenosové funkce

Parametr R musí být kladné reálné číslo. Při volbě zakončení NDP open musí být směr zpracování front a pro sudý stupeň filtru volit strukturu T , pro lichý stupeň filtru, je třeba zvolit strukturu PI . Při zakončení short je třeba zvolit směr zpracování rear a strukturu T .

Description:

Funkce počítá prvky LC příčkového filtru typu NDP pomocí postupného odštěpování z kaskádní matice, která je sestavena z provozního činitele přenosu a charakteristické funkce.

Způsob realizace a výsledná struktura filtru závisí na přítomnosti posledního parametru zeros . Tento parametr je nutné zadat pro správný výpočet při návrhu NDP pomocí inverzní Čebyševovy aproximace a Cauerovy aproximace.

Návratovou hodnotu funkce tvoří tabulka s popisem filtru.

Tabulka s popisem filtru je tvořena strukturou table , která má následující položky: type , R1 , R2 a dále pak položky 1..n , kde n je rovno stupni filtru (stupeň aproximace order ).

Položka type může nabývat v závislosti na způsobu zakončení těchto hodnot: LC_NLP_common , LC_NLP_open a LC_NLP_short .

Položky R1 , R2 závisí na parametru R , na způsobu zakončení. Pro zakončení naprázdno je R2 rovno nekonečno a R1 je rovno R . Při zakončení nakrátko je R1 rovno nule a R2 je rovno R . Při standardním zakončení je R1 rovno R a R2 může být rovno R1 , ale pro některé případy může být jak větší tak menší než R1 .

Položky 1..n popisují zapojení jednotlivých větví filtru v postupném pořadí odpovídající číslum položek ve směru za předu od zdroje a tvoří je opět struktura table s následujícími položkami: Z , elements a orientation .

Položka orientation určuje orientaci větve a může nabývat hodnot direct (podélně) nebo shunt (příčně). Tyto hodnoty se střídají. Pokud je jedna větev podélně, následující je příčně a naopak.

Položka elements je tvořena množinou set a obsahuje prvky větve a jejich hodnoty.

Položka Z je rovna impedanci větve v symbolické podobě. To určuje zapojení prvků větve uvedených v položce elements . Impedance zde může nabývat následujících hodnot (pokud proměnná provozního činitele přenosu a charakteristické funkce je s):

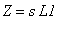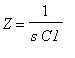pro podélný induktor, Z = 1/(s*C1)

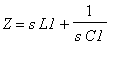pro příčný kapacitor, Z = s*L1+1/(s*C1)

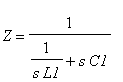pro příčný sériový rezonanční obvod a Z = 1/(1/(s*L1)+s*C1)

pro podélný paralelní rezonanční obvod.

Info level:

Změnou proměnné infolevel[syntfil] dostanete podrobnější výsledek.

infolevel[syntfil] =

2 - vypsání výsledné zbytkové matice, typu NDP, hodnot zakončovacích rezistorů a jednotlivých bloků NDP

3 - jako úroveň 2 + vypsání výchozí kaskádní matice

4 - jako úroveň 3 + vypsání dílčích matic, které vzniknou vždy po odštěpení dvou dílčích větví příčkové struktury

5 - jako úroveň 4 + vypsání hodnot dílčích prvků jednotlivých větví příčkové struktury

Example:

> with(syntfil):

Provozní činitel přenosu a charakteristická funkce pro normovanou Butterworthovu aproximaci

> pol,chpol:=s^3+2*s^2+2*s+1,s^3;

> DroppNLP(common,1,front,T,pol,chpol);

Výpočet inverzní Čebyševovy aproximace

> G,Phi,zeros:=InvChebyshev(3,1.4,1,s);

> elems_nlp:=DroppNLP(common,1,front,PI,G,Phi,zeros);

$elems_nlp := TABLE([1 = TABLE([elements = {C1 = .4980605765}, Z = 1/(s*C1), orientation = shunt]), 2 = TABLE([elements = {L1 = .9961201436, C1 = .3841434827}, Z = 1/(1/(s*L1)+s*C1), orientation = direc...$
$elems_nlp := TABLE([1 = TABLE([elements = {C1 = .4980605765}, Z = 1/(s*C1), orientation = shunt]), 2 = TABLE([elements = {L1 = .9961201436, C1 = .3841434827}, Z = 1/(1/(s*L1)+s*C1), orientation = direc...$
$elems_nlp := TABLE([1 = TABLE([elements = {C1 = .4980605765}, Z = 1/(s*C1), orientation = shunt]), 2 = TABLE([elements = {L1 = .9961201436, C1 = .3841434827}, Z = 1/(1/(s*L1)+s*C1), orientation = direc...$
$elems_nlp := TABLE([1 = TABLE([elements = {C1 = .4980605765}, Z = 1/(s*C1), orientation = shunt]), 2 = TABLE([elements = {L1 = .9961201436, C1 = .3841434827}, Z = 1/(1/(s*L1)+s*C1), orientation = direc...$
$elems_nlp := TABLE([1 = TABLE([elements = {C1 = .4980605765}, Z = 1/(s*C1), orientation = shunt]), 2 = TABLE([elements = {L1 = .9961201436, C1 = .3841434827}, Z = 1/(1/(s*L1)+s*C1), orientation = direc...$

Sestavení přenosové funkce z tabulky s popisem filtru

> MakeH(elems_nlp);

MakeH, ElemsLP, ElemsHP, ElemsBP, ElemsBP2, ElemsBPm, ElemsBP2m, ElemsBS, ElemsBSm